概率论与数理统计
2024学年第二学期概率论与数理统计期末复习
**理论复习链接:**https://saurlax.netlify.app/blog/probability-and-statistics/ 或 https://saurlax.com/blog/probability-and-statistics/
课后习题&课后作业复习
第一次作业
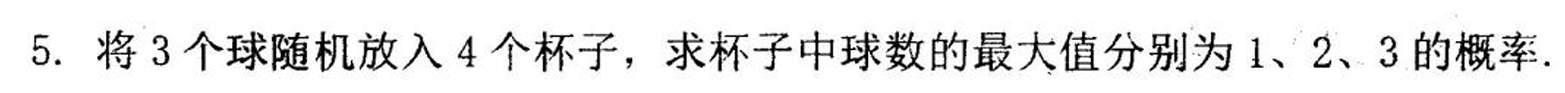
| 最大球数 | 概率 |
|---|---|
| 1 | 3/8 |
| 2 | 9/16 |
| 3 | 1/16 |
将每个球,每个杯子都视为不同的,分母是4^3,分子就正常求解即可

| 题号 | 答案 |
|---|---|
| 1 | 1/8 |
| 2 | (2+2In2)/4 |
几何概率求解即可

几何概率求解,答案为5/9
第二次作业

前推后 [ 必要性证明 ]:A,B相互独立的性质
后推前 [ 充分性证明 ]:根据原式推出P(A|B) = P(A|_B),再代回P(A)的全概率公式可以推出P(A) = P(A|B),得证
第三次作业
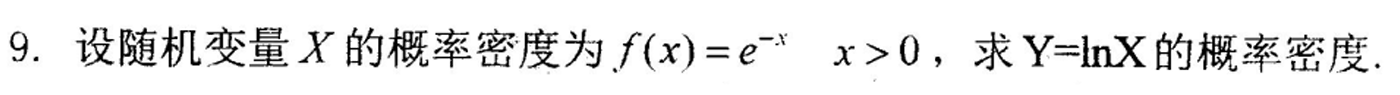
Fy( y ) = P( Y =< y ) = P( Inx =< y ) = P( X =< e^y),随后由题求出Fy( y ) 再求导即可求出Y的概率密度

思路方法与上一题相同,先求出Fy(y)即可

仍旧与之前相同
第四次作业
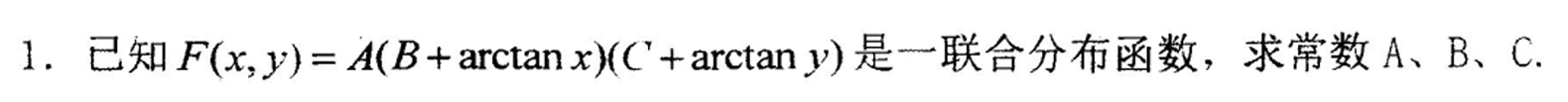
联合分布函数的性质,F(-∞,y) = 0 ,F(x,-∞) = 0 ,F(+∞,+∞) = 1即可求出各个未知数的值

过程就是正常计算,但是中间要用e^x的泰勒展开化简,这在概率中比较常见
第五次作业

(1) 积分后结果为1
(2) 从-∞作二重积分到x,y得到F(X,Y)
(3)作图后进行二重积分
(4)计算边际分布(密度)函数

求出x,y的联合概率密度函数,再FS(s)的表达式写出,由此得到二重积分的积分区域,最后再对s求导即可得到fS(s)

先求分布函数,再求导获得密度函数

用表达式直接算

二维连续型随机变量函数的分布列
第六次作业
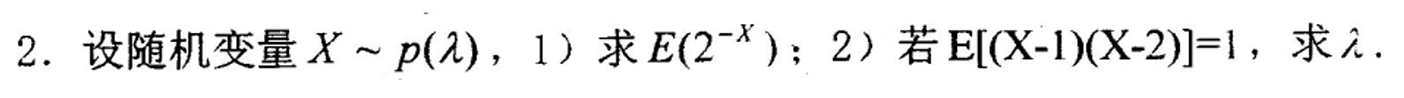
泰勒展开化简得到结果
第七次作业
暂无
第八次作业

大数定理
Yi = Xi^2 ,Y1,Y2,Y3……相互独立且同分布,有切比雪夫大数定理可知,依概率收敛于E(Yi) 所以服从大数定理
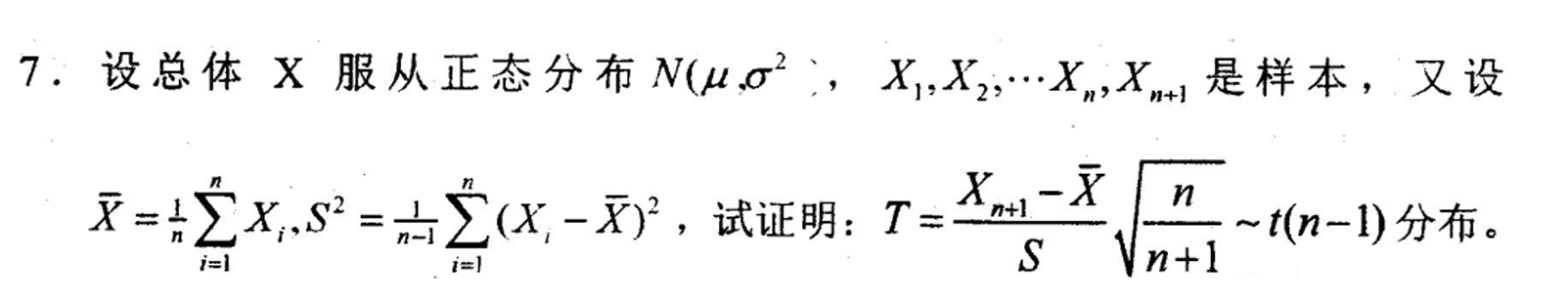
Xn+1 - _X 先标准化 再通过抽样正态分布的性质(卡方) ,最后构造出了 t ( n-1 ) 分布
第九次作业
各种性质的正态分布

**(1) 利用正态分布的公式计算 **
(2) 选取单正态分布的性质来计算
(3) 问题(2)中带入关系式即可
第十次作业
暂无
第十一次作业

单调的极大似然估计函数

期末自测
期末自测1:

题目叙述有误,f(x)关于 x = c 对称是 f(c-x) = f(c+x)
EX = ∫ xf(x) dx = ∫ [ c- (c - x) ]f(x) dx = c∫ f(x) dx - ∫ (c-x)f(x) dx
**= c - ∫ (c-x)f(x) dx = c - ∫ yf(c-y) dy = c -∫ yf(c+y) dy = c - ∫ (t-c)f(t) dt **
= c - [ EX - c ] = 2c -EX 得证

(1) 不独立
(2) 计算表达式为 2 -> +∞ ∫ fY|X ( y | x=3 ) dy

(1) 选取正态分布统计量,查表中数据计算出置信区间
(2) 作出假设和备择假设,选取正态分布统计量,查表中数据计算拒绝域,再带入实际值确定是否在拒绝域中
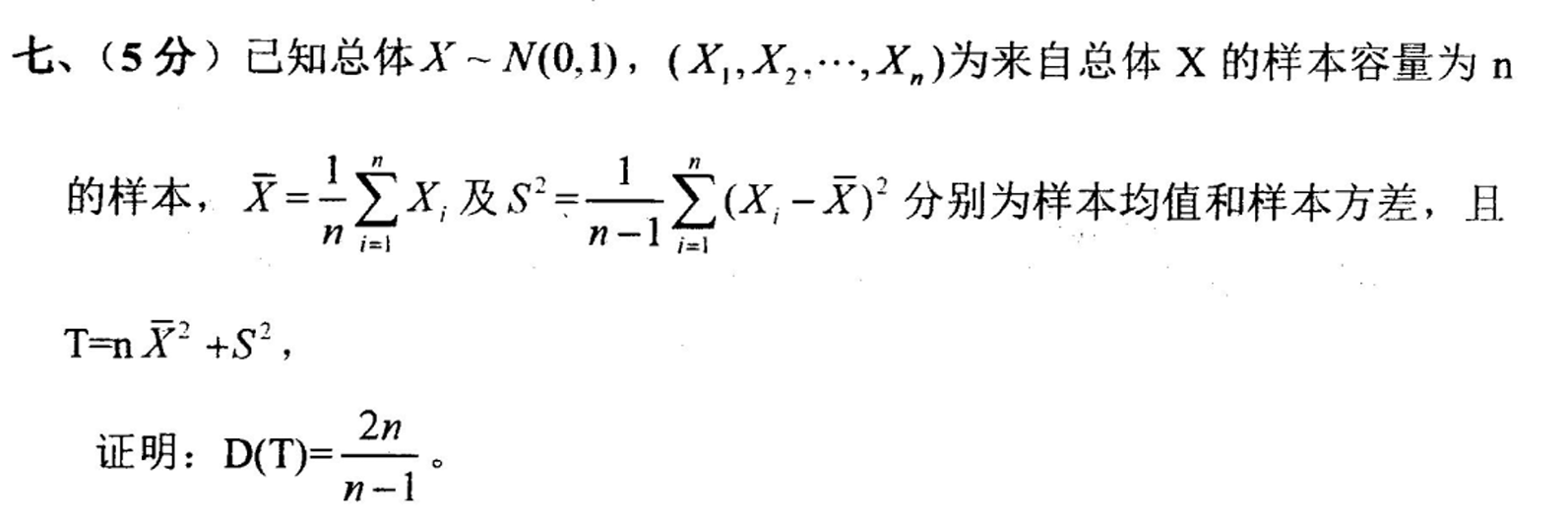
_X ~ N (0,1/n) E( _X^4) = (1/n)^2 * 3!! = 3/n^2推出D(X) = 2/n^2 由单正态分布统计量的性质可知 D(n-1)S^2 = 2(n-1) 带入原式计算即可得到结果
期末自测2:

(1) 建议按照之前的方法做,直接用公式不太会
(2) 都转化为x的范围然后求出对应的概率即可,其实最后只要求x-1/2的分布函数即可

n个 0 - 1 分布的随机变量求和设为X(匹配数),且随机变量之间不相互独立
注意求方差时,不独立的变量要加上协方差

先进行标准化,再将标准化后的变量的平方求和,最后通过大于等于0即可得到不等式

(1) 构造单正态总体的性质中合适的分布,然后查表获得对应的置信度的分位点,最后解出置信区间,端点相减
(2) 做出假设和备择假设(备择假设一定是小概率),确定利用哪个性质,最后查表,并带入值与之比较,确定是否在拒绝域内

先求出极大似然估计函数,再求导令其等于0得到极值点即可