微积分下
微积分下
[TOC]
期中考试复习 [ 无穷级数,向量代数与空间解析几何,多元函数微分学及其应用 ]
无穷级数
5.1 常数项级数的概率与基本性质
课后简单习题回顾练手

| 题号 | 提示 |
|---|---|
| 1 | 求和 |
| 2 | 裂项求和 |
| 3 | 裂项求和 |
| 4 | 求和 |

| 题号 | 提示 |
|---|---|
| 1 | 两个收敛级数 |
| 2 | 取极限第n项不为0 |
| 3 | 取极限第n项不为0 |
| 4 | 两个收敛级数 |
一个收敛级数与一个发散级数逐项相加所得级数一定发散,两个发散级数逐项相加所得的级数可能收敛

拆分为奇偶项再作化简
课堂习题
1.

answer

2.

answer
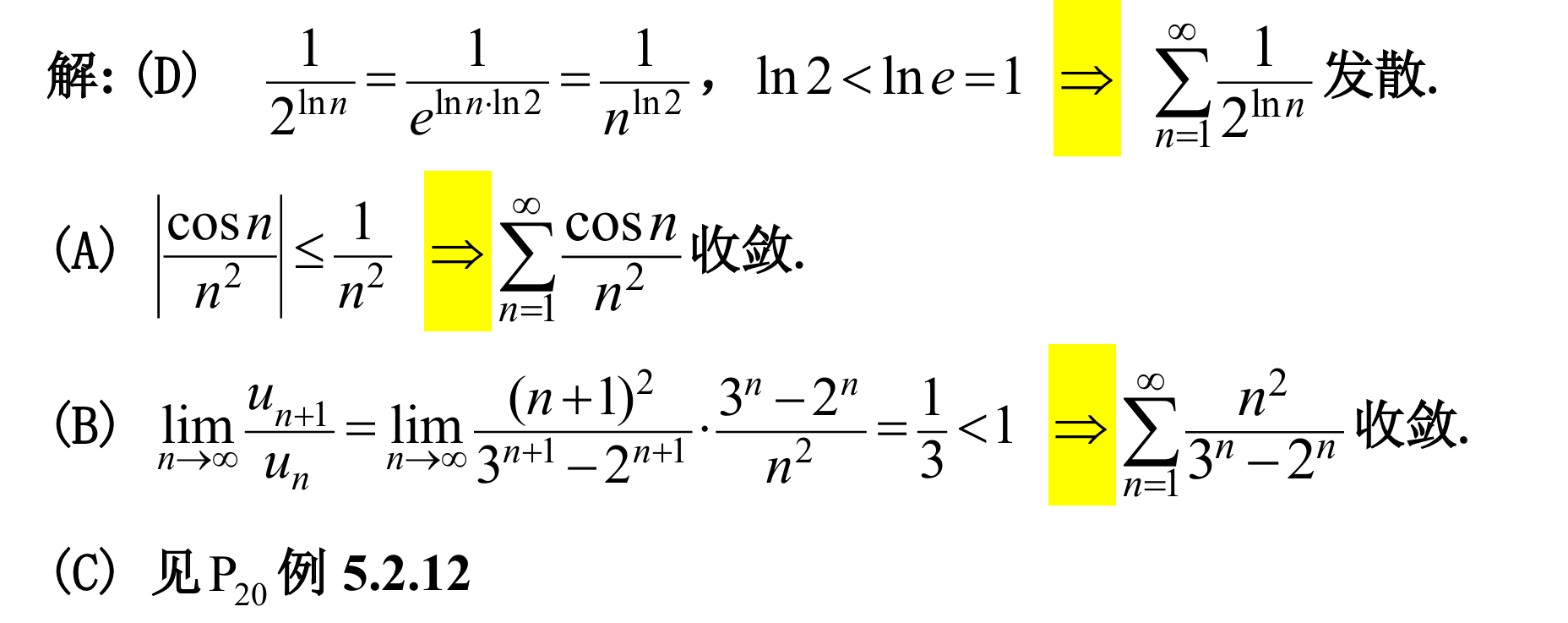
3.
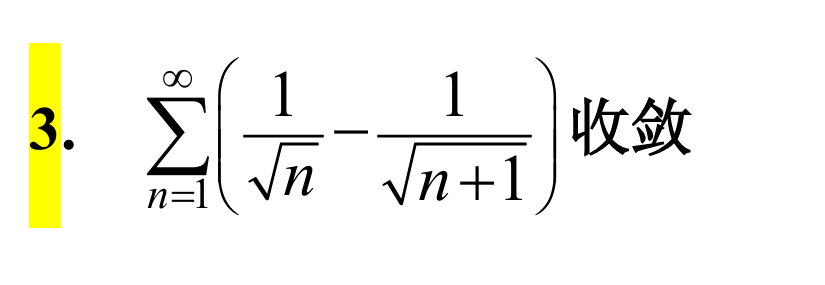
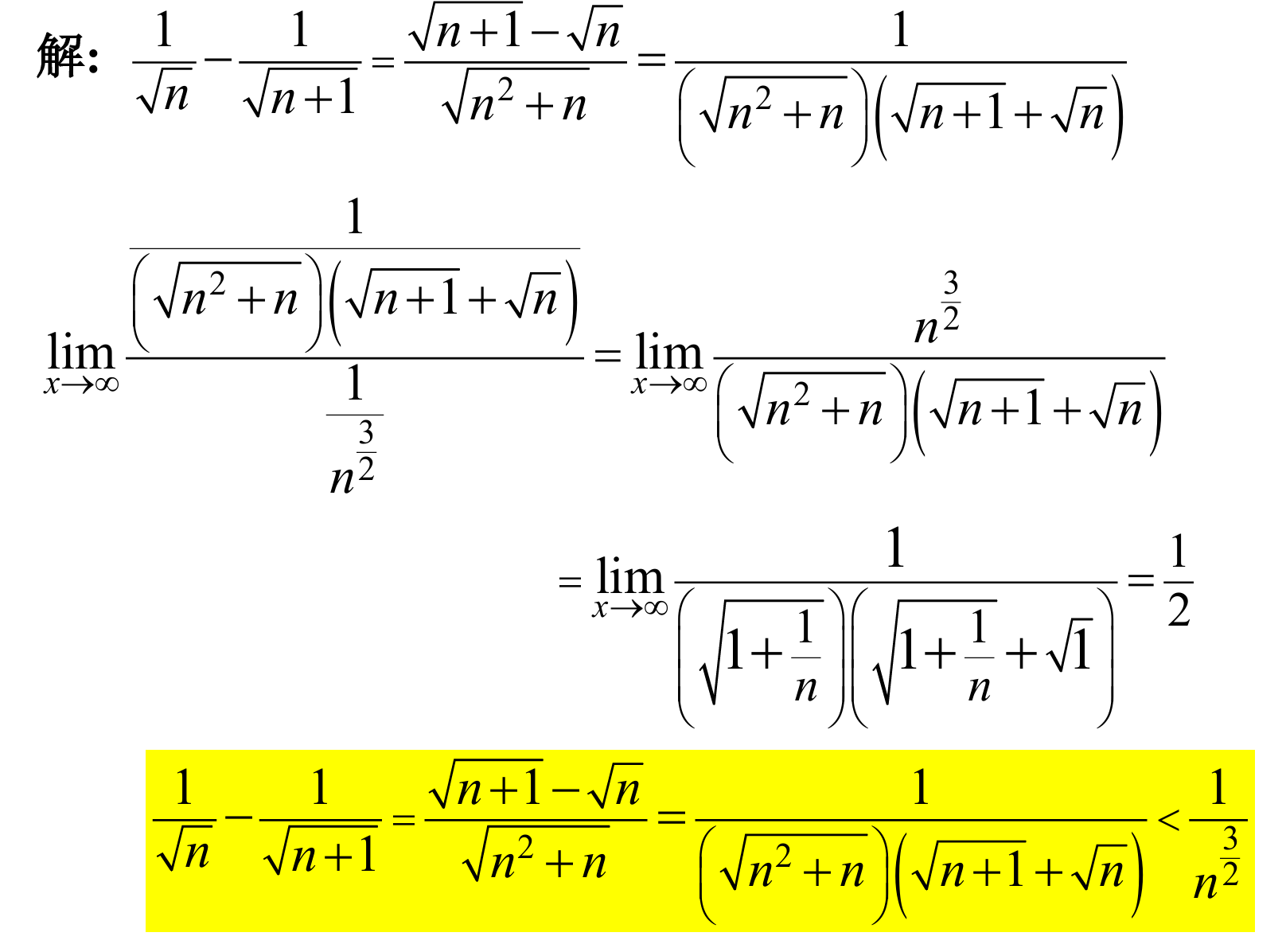
answer
4.
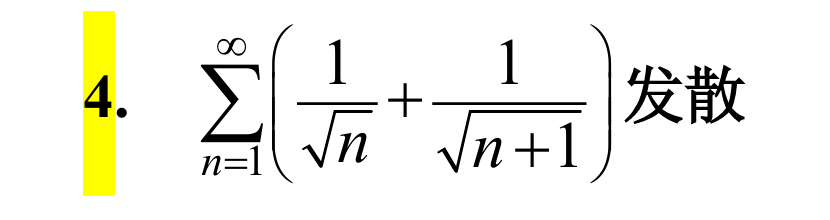
answer
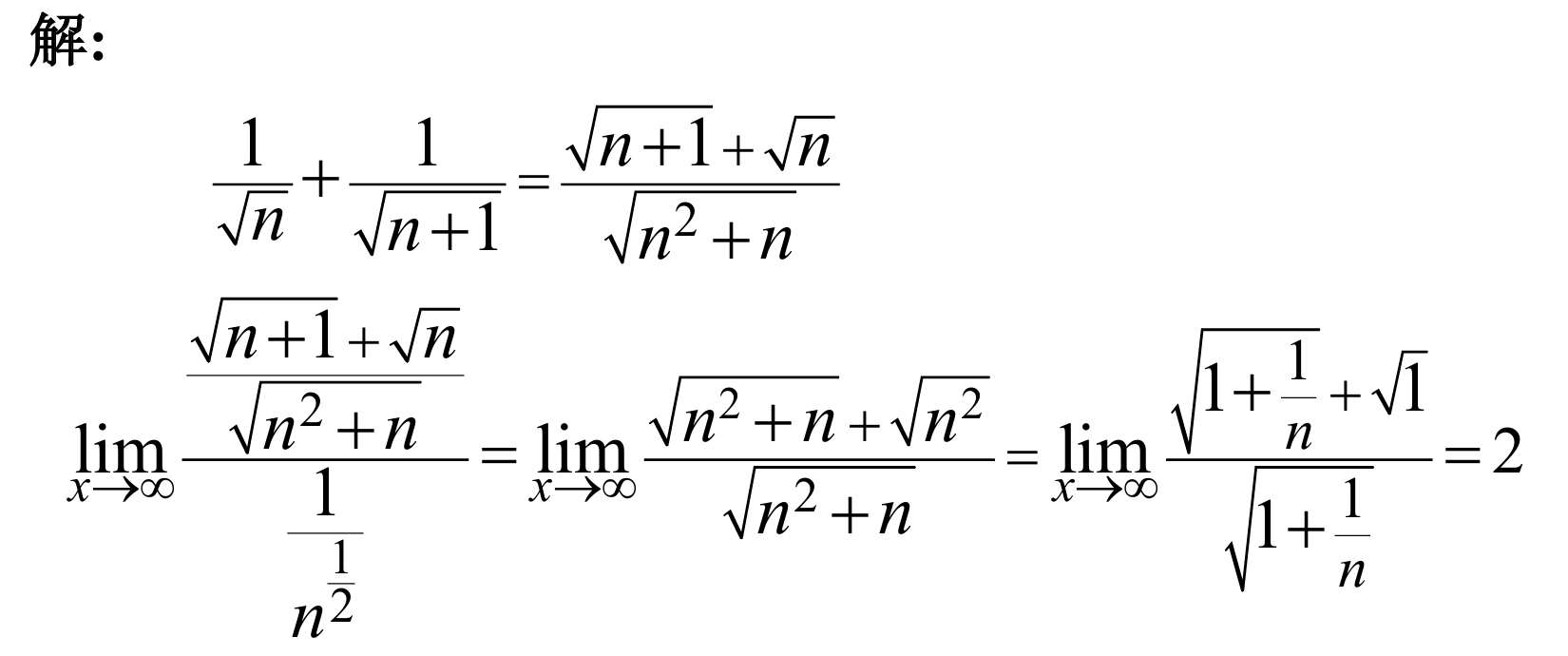
5.
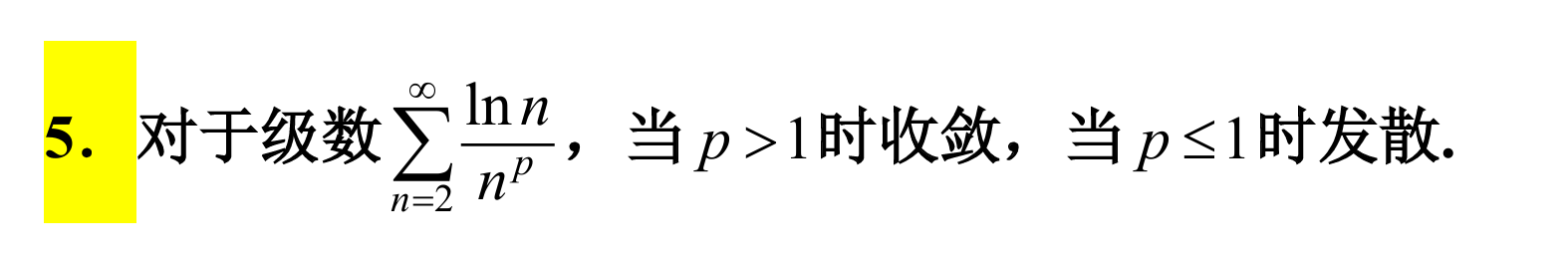
answer

6.

answer
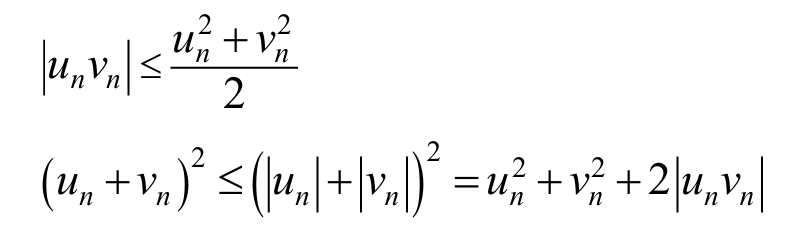
7.

answer

8.

answer
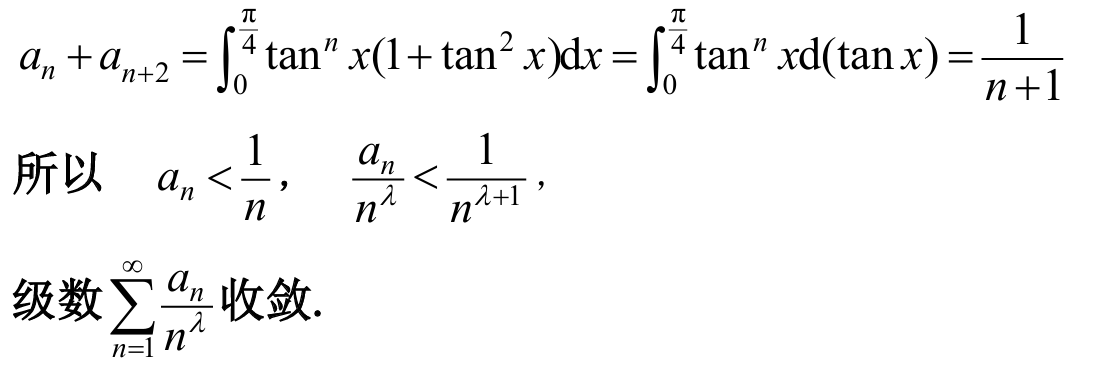
9.
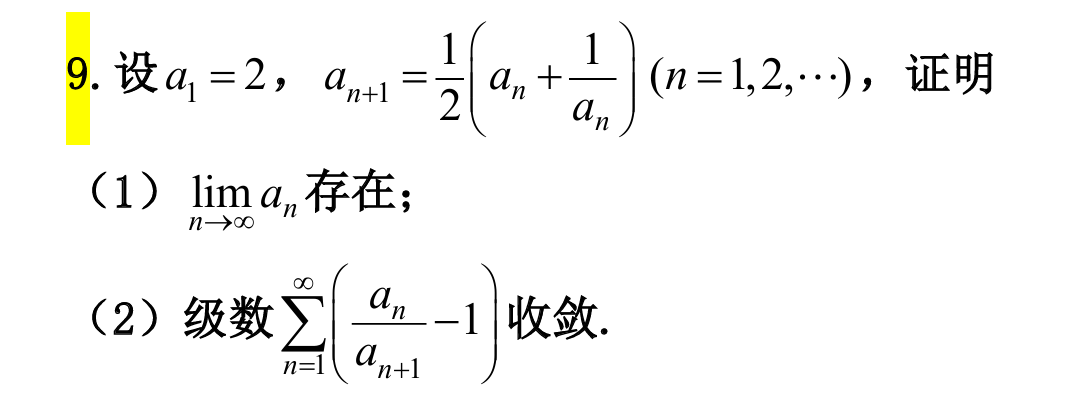
answer

5.2 正项级数敛散性的判别法
课后简单习题回顾练手

比值判别法



基本不等式 + 比较判别法


| 题号 | 提示 |
|---|---|
| 1 | 举一个P级数的例子 |
| 2 | 正确,证明在5.1的课堂习题末尾 |
| 3 | 前对,后错 [ 0 ,1交错的级数 ] |
5.3 任意项级数敛散性判别法
课后简单习题回顾练手

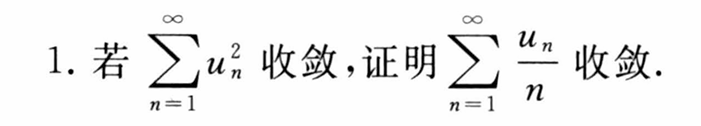
基本不等式

方法一

方法二

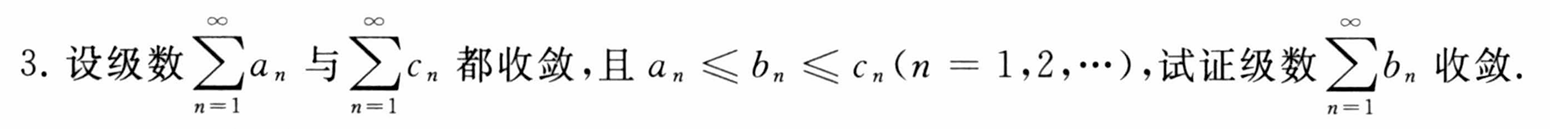
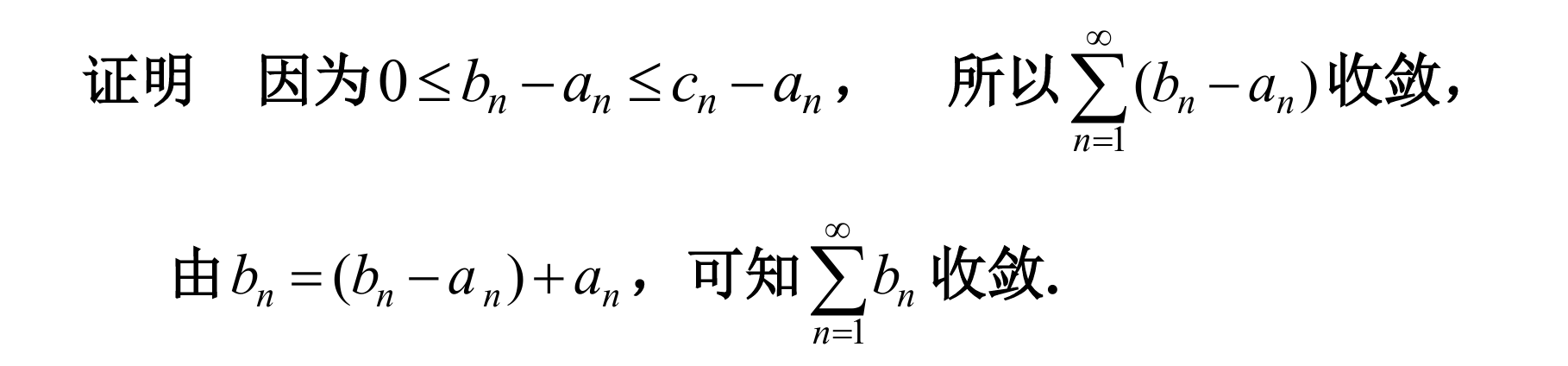

| 题号 | 提示 | 答案 |
|---|---|---|
| 1 | 绝对收敛 | |
| 2 | 等价无穷小【 比较判别法 】 | 条件收敛 |
| 3 | 绝对收敛 | |
| 4 | 发散 | |
| 5 | 绝对收敛 |
课堂习题
1.

answer:D
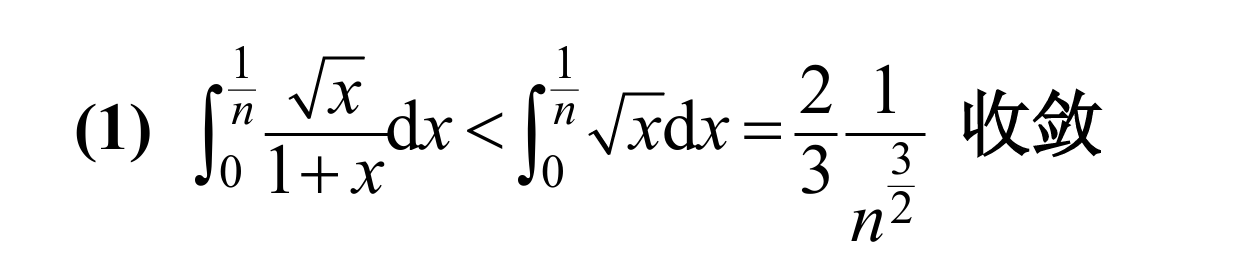
2.

answer
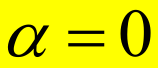
3.

answer
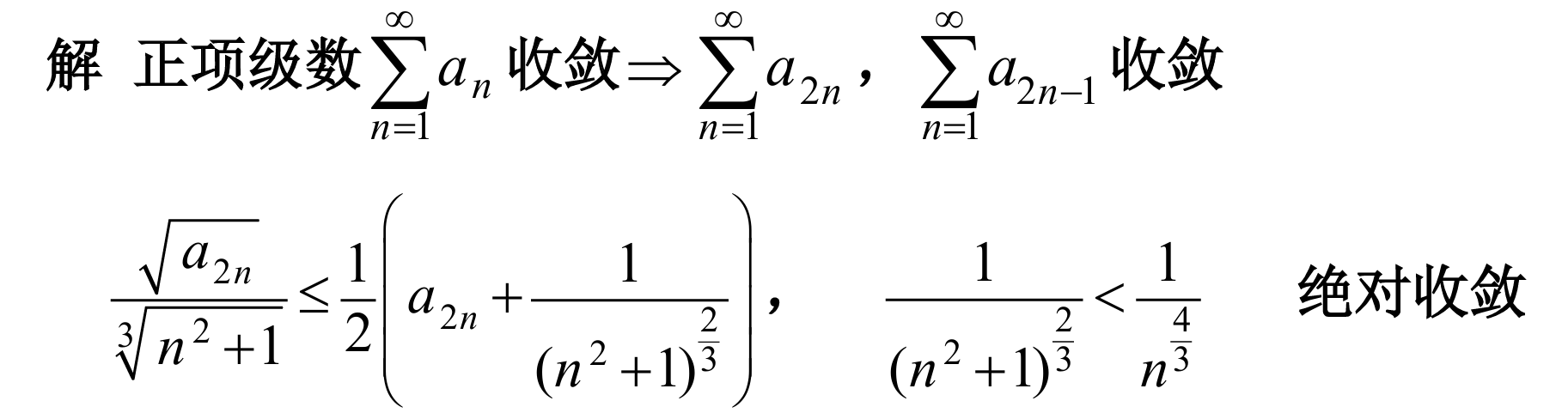
4.

answer
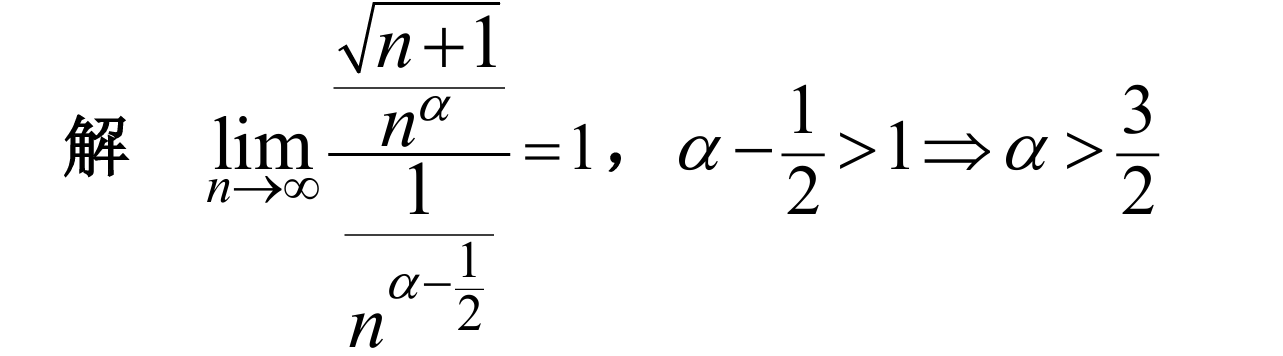
5.

answer


6.

answer
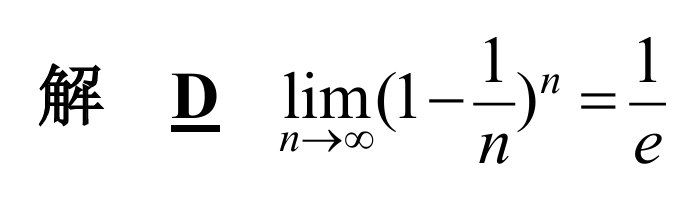
7.

answer
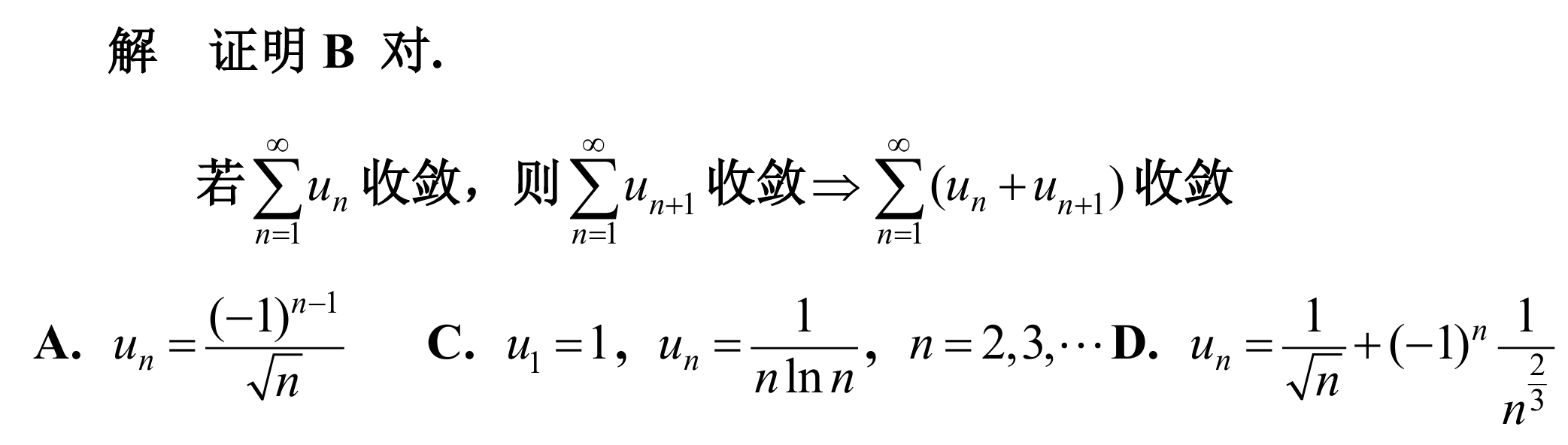
8.

answer

9.

answer

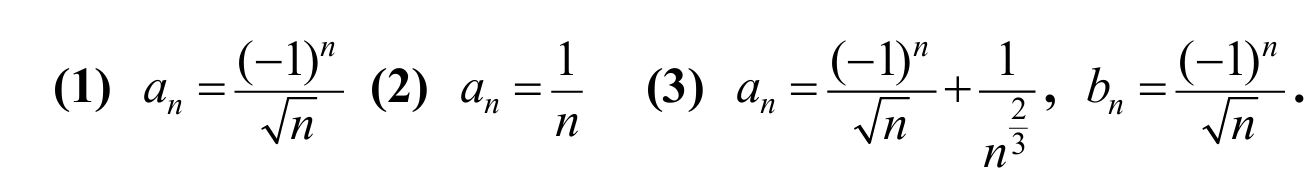
10.

answer
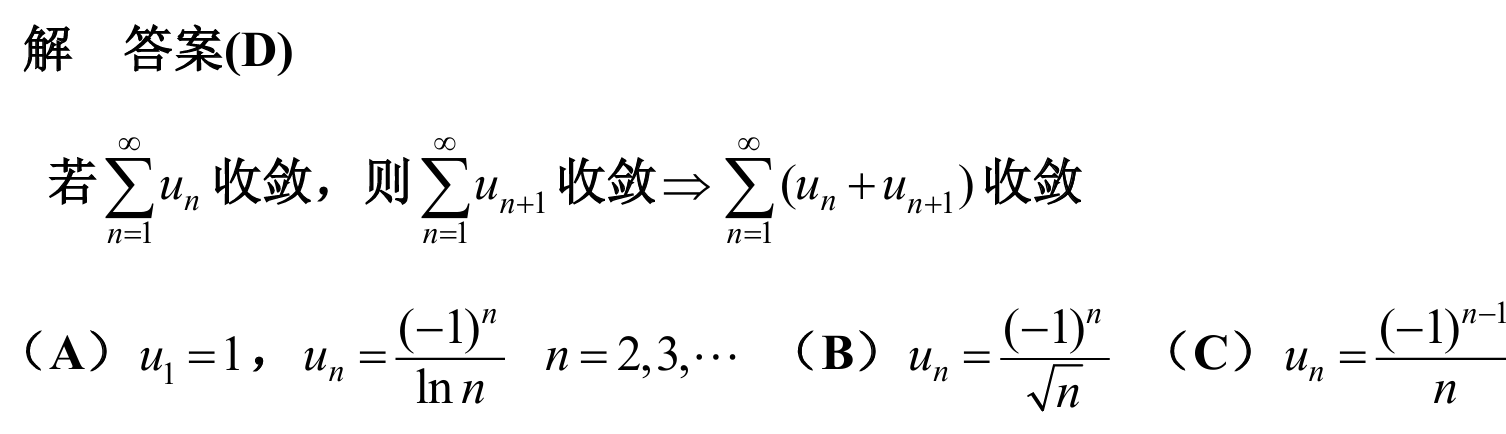
11.

answer
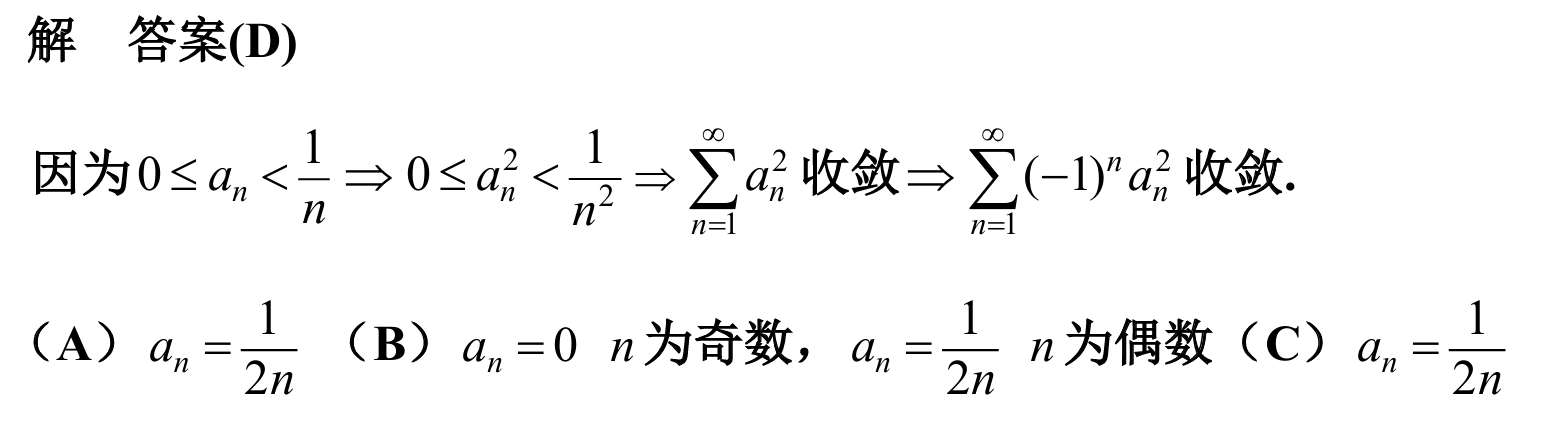
12.

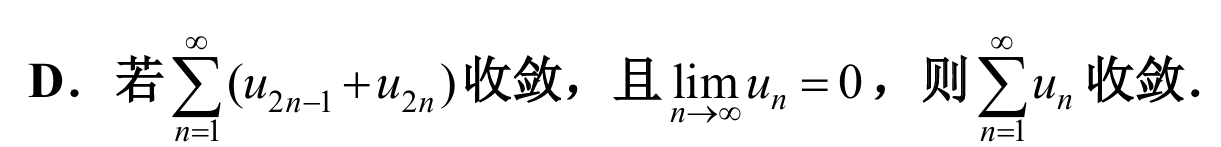
answer

13.

answer

14.

answer
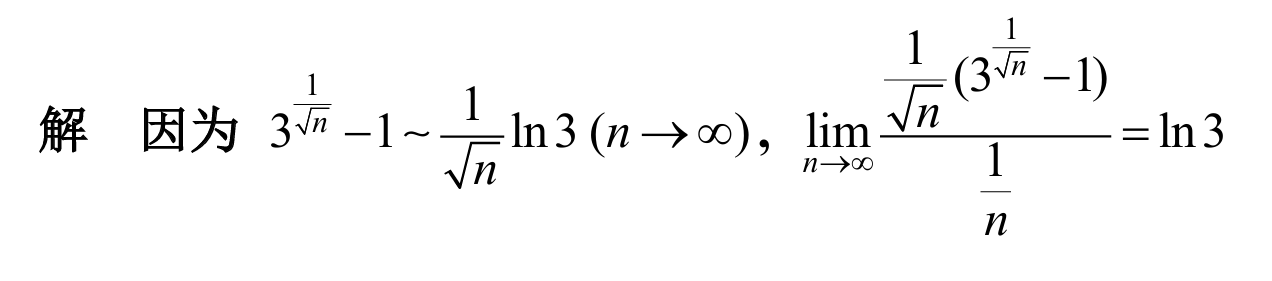

15.
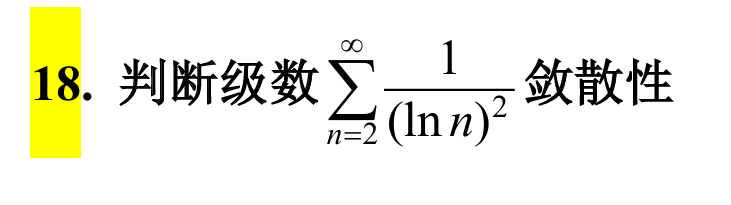
answer

5.4 幂级数
课后简单习题回顾练手

| 题号 | 收敛域 | 收敛范围 |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |

| 题号 | 收敛域 | 收敛半径 |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |




多元函数微分学及其应用
可微,连续,可偏导之间的关系
7.1多元函数的基本概念
课后简单习题回顾练手
提示写在自己的课本上了

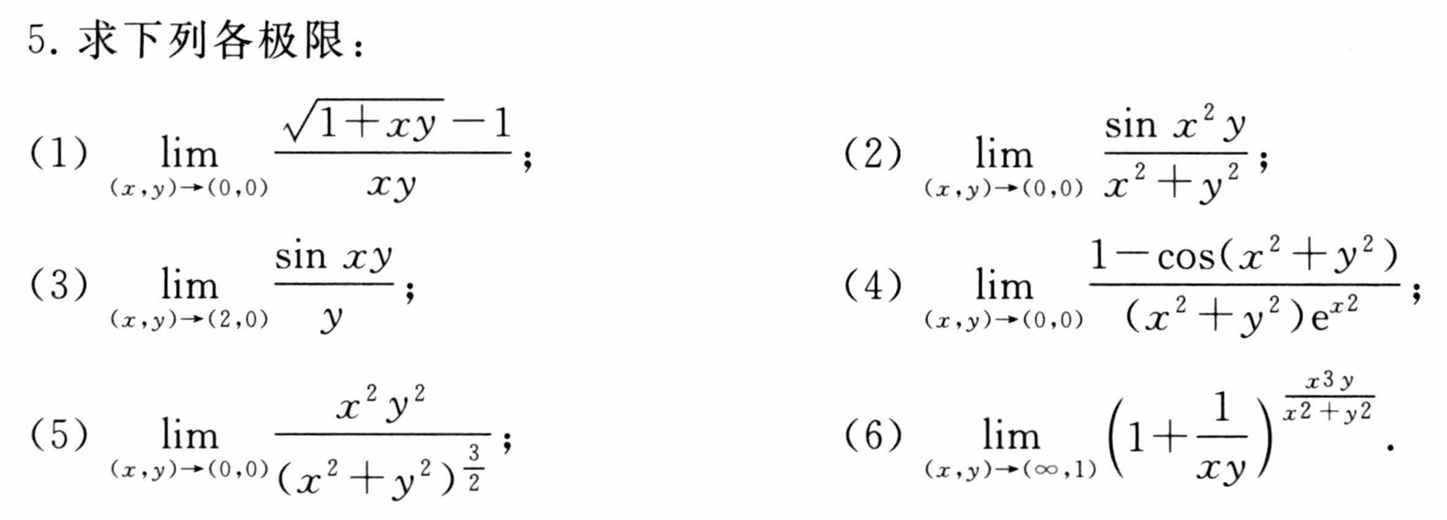
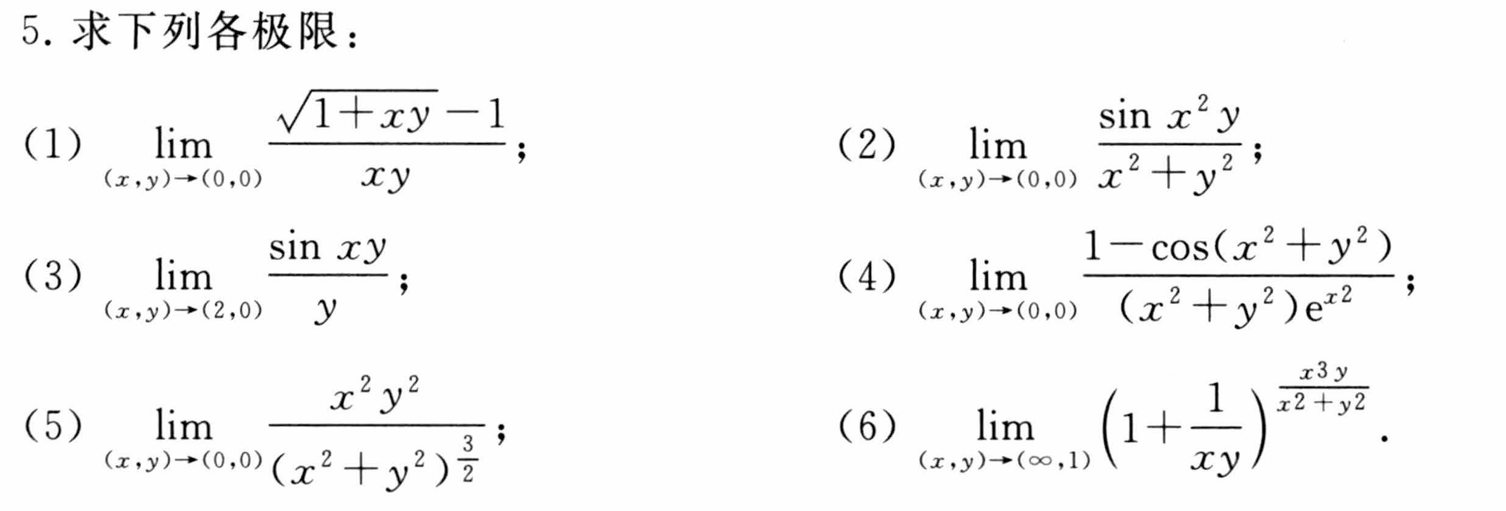
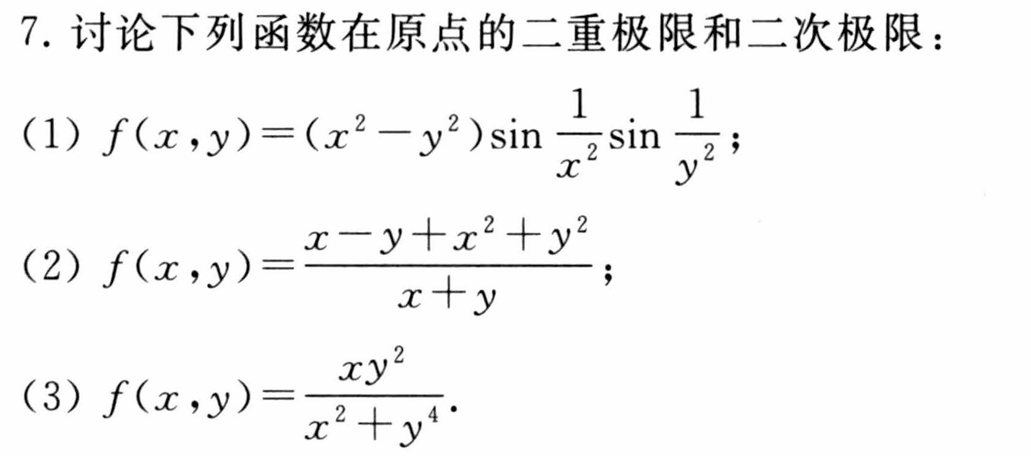
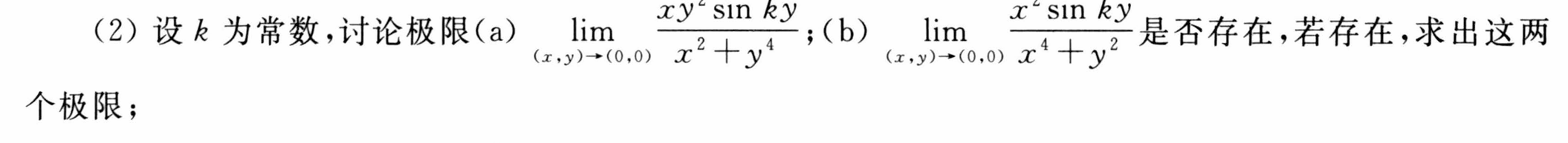
7.2 偏导数与高阶偏导数
课后简单习题回顾练手
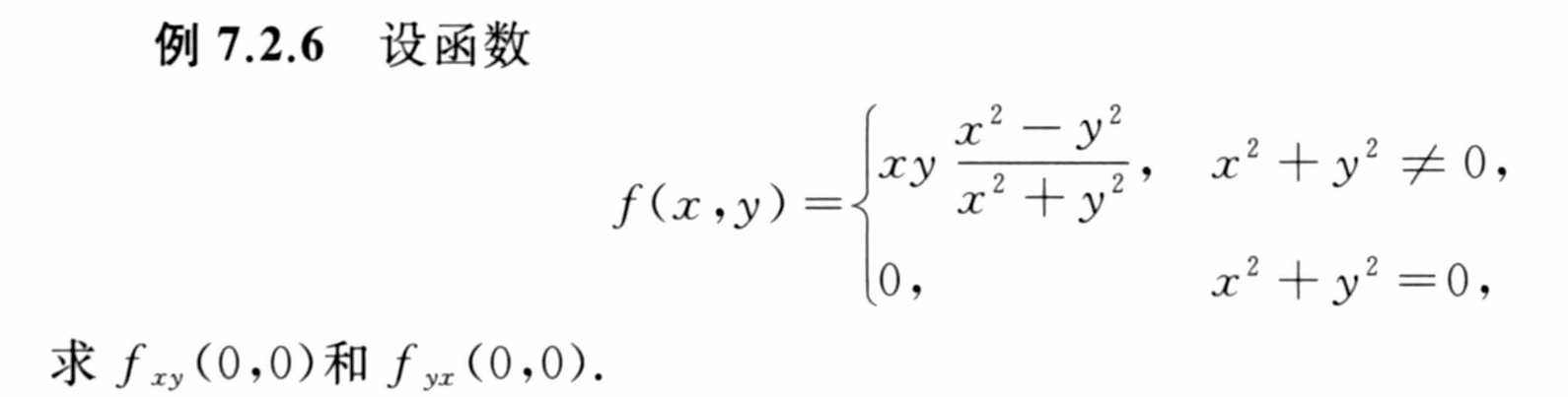

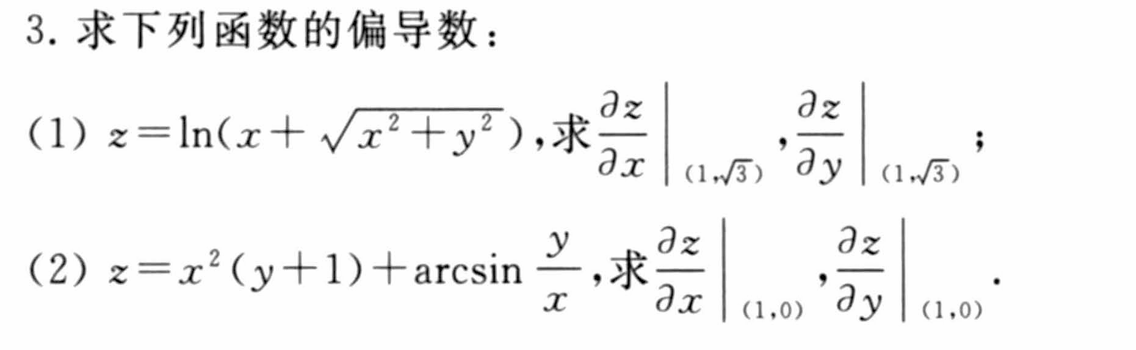
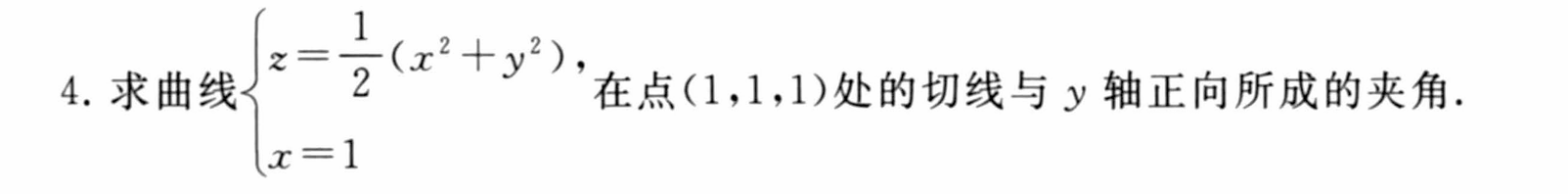
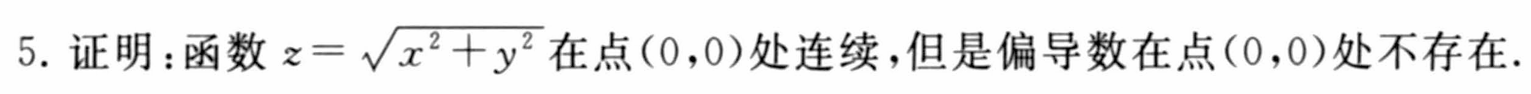


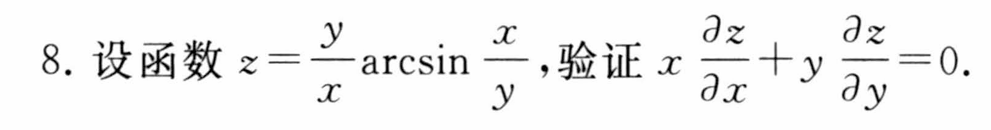
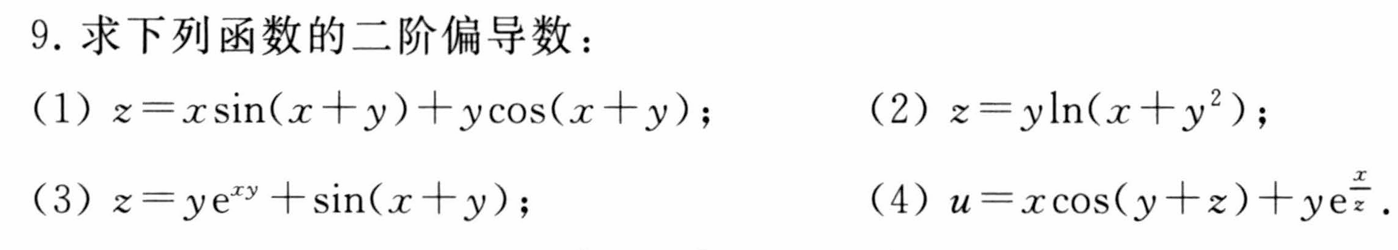
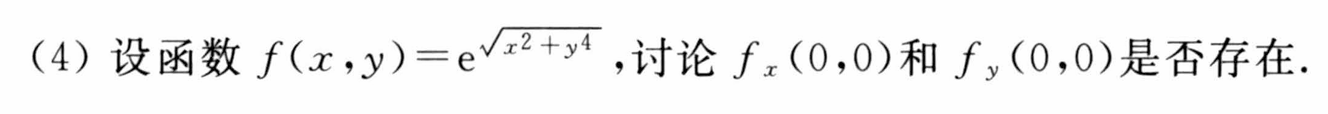
7.3 全微分及高阶全微分
课后简单习题回顾练手
函数不可微的证明方式


全微分代替全增量估算
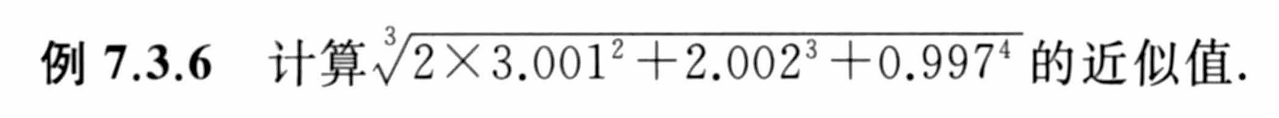
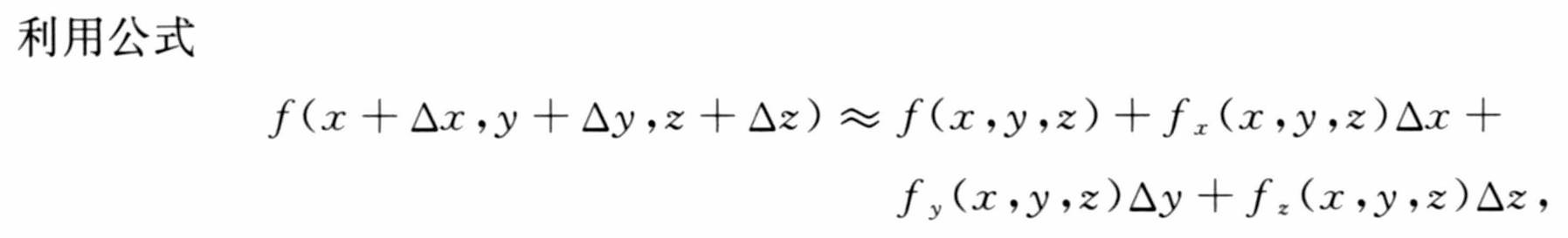
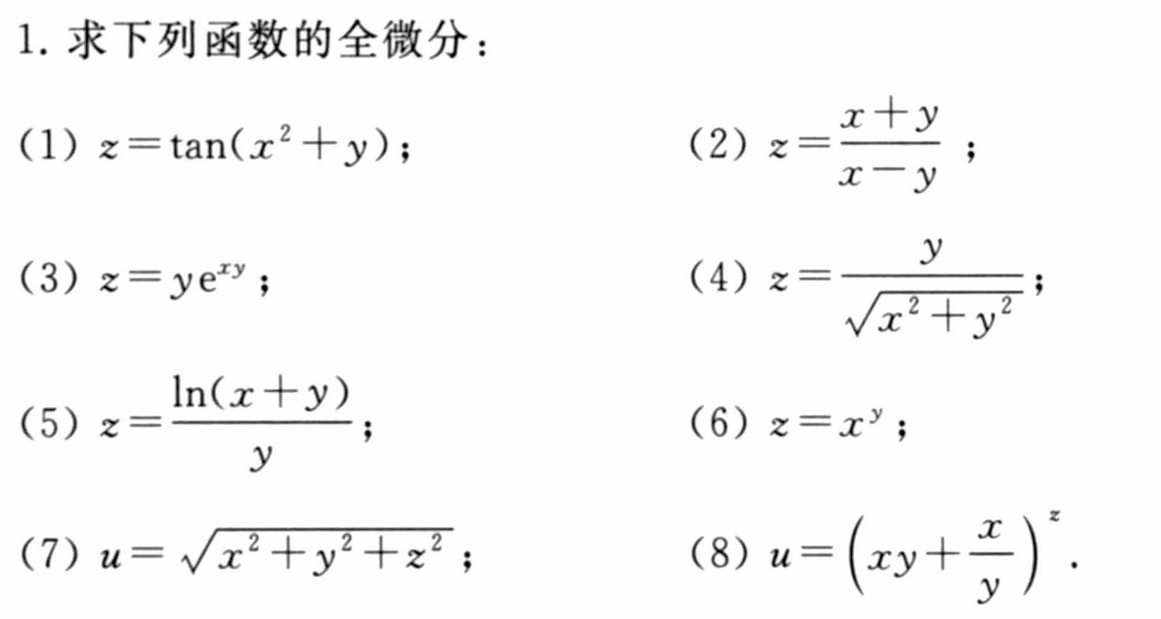
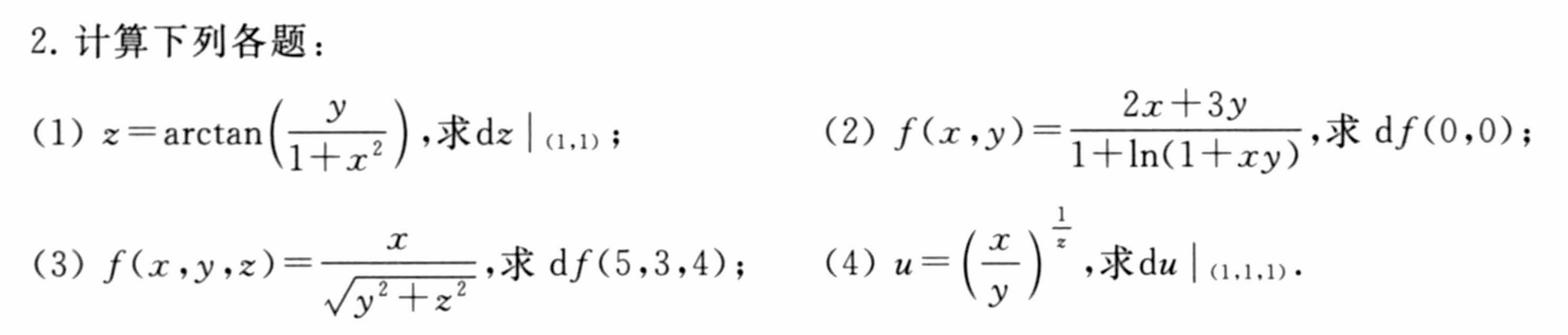
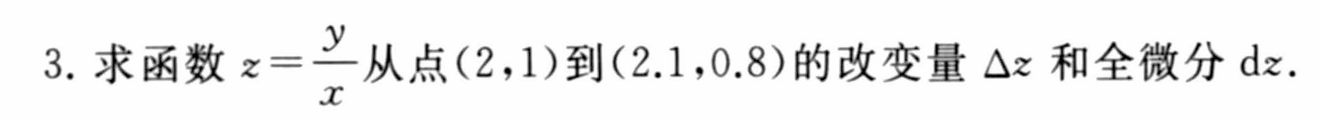
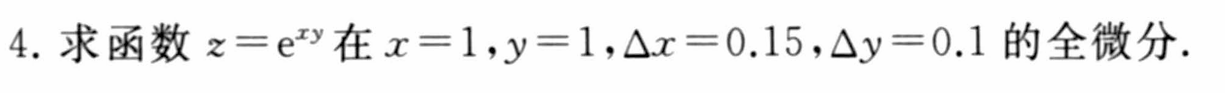


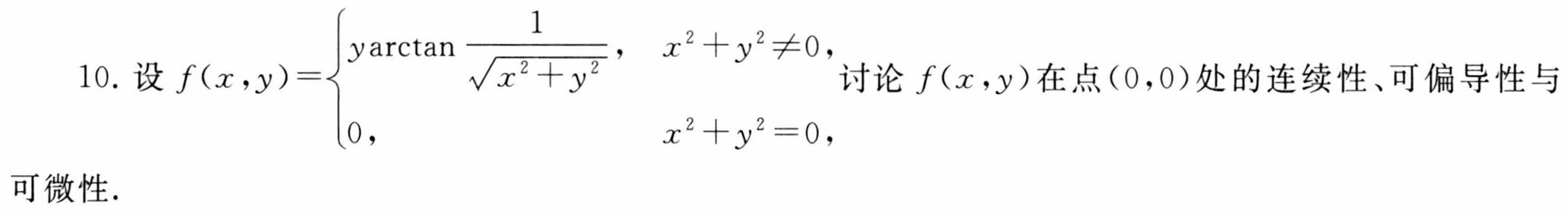
10.连续可微且可偏导
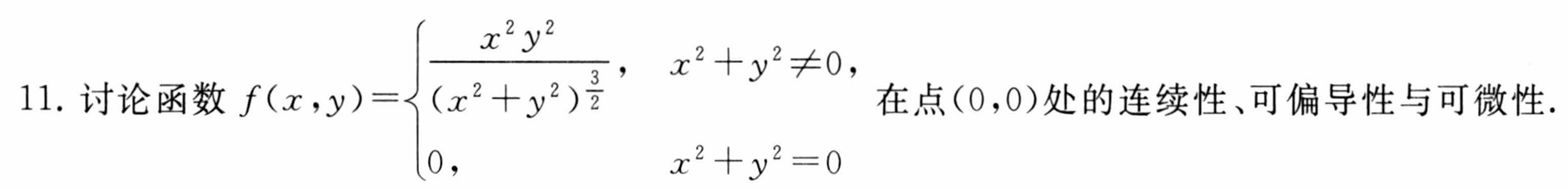
11.连续可微且不可偏导
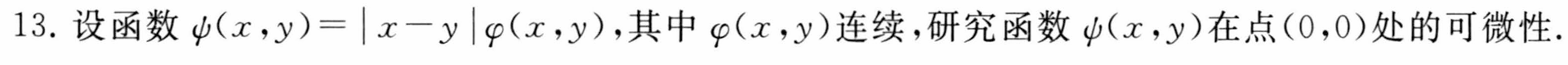
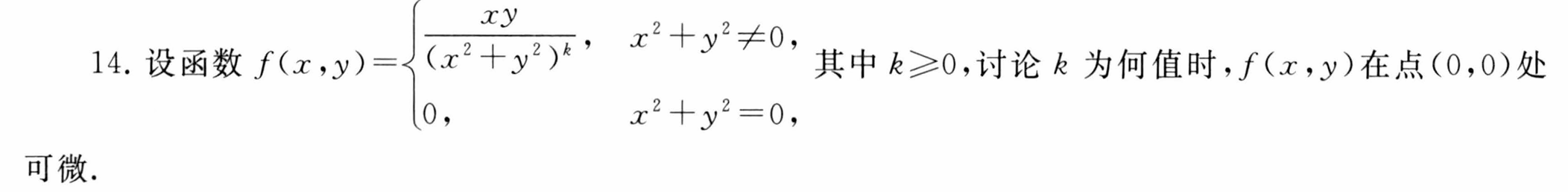



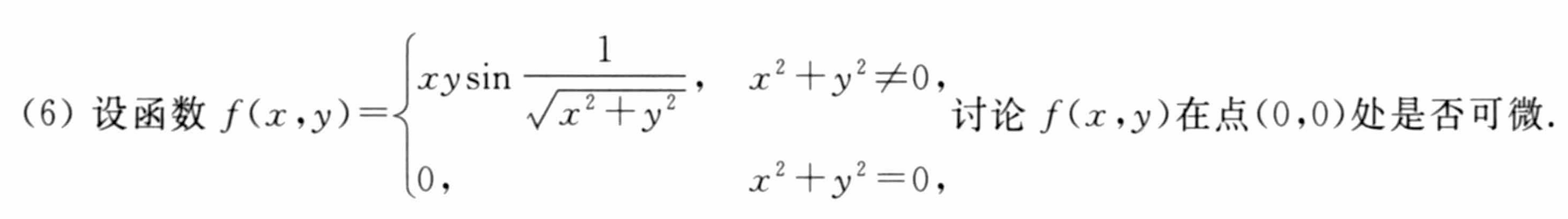
7.4 多元复合函数微分法
课后简单习题回顾练手
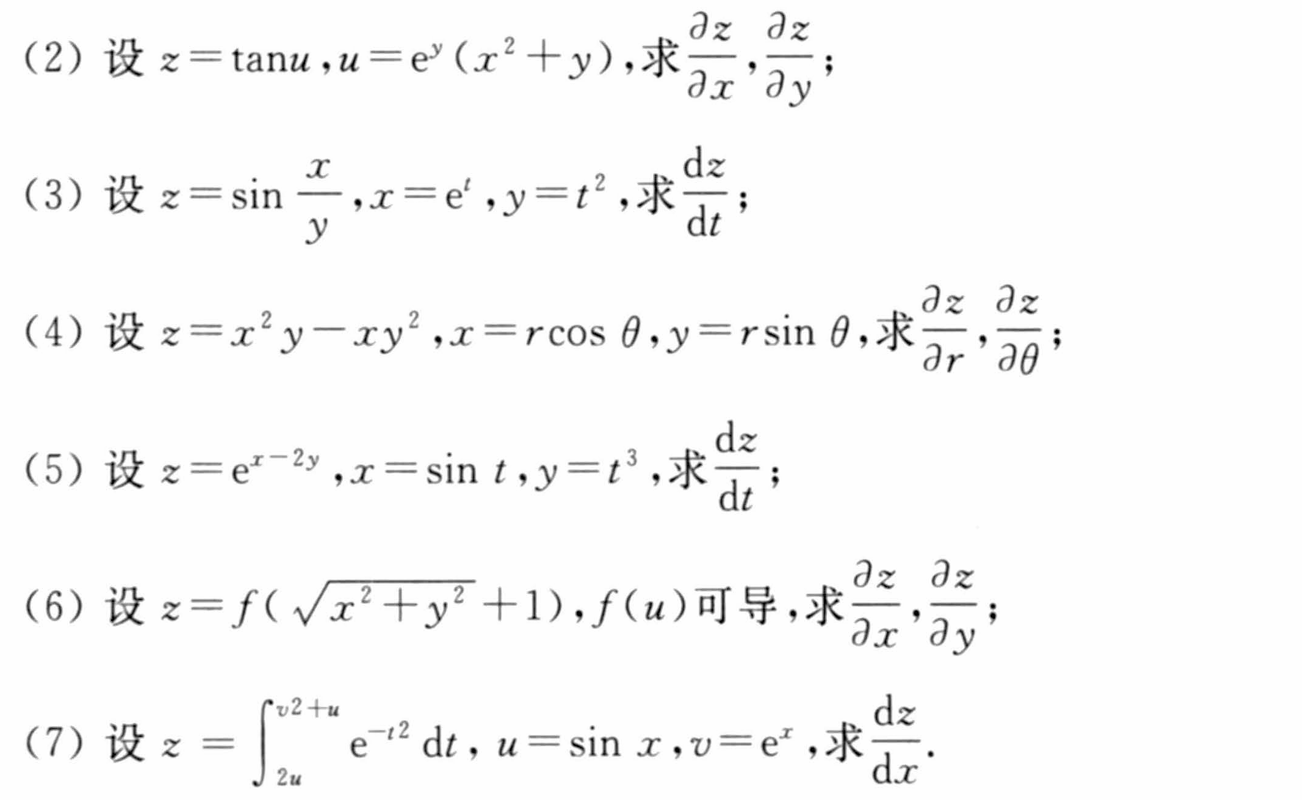


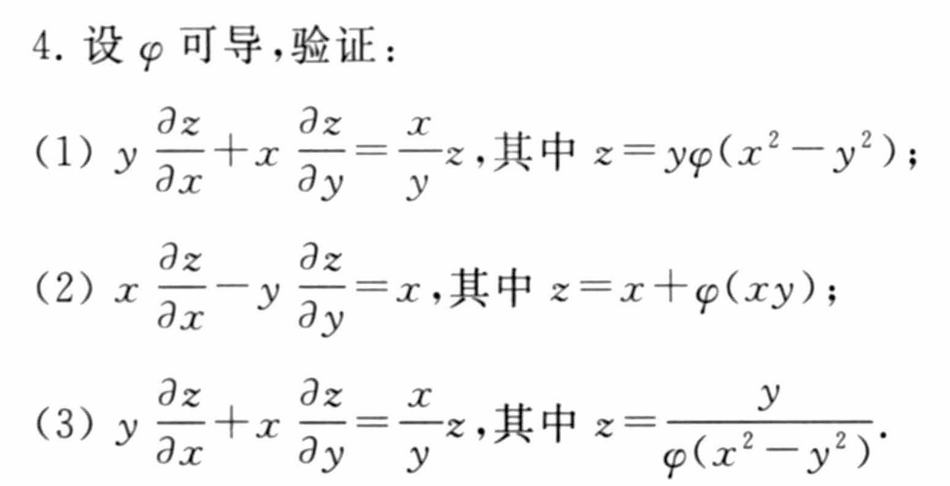
隐函数存在定理一

隐函数存在定理二

7.5 方向导数与梯度
课后习题简单回顾



7.7 偏导数在几何中的应用
课后习题简单回顾

利用隐函数存在定理求出切向向量
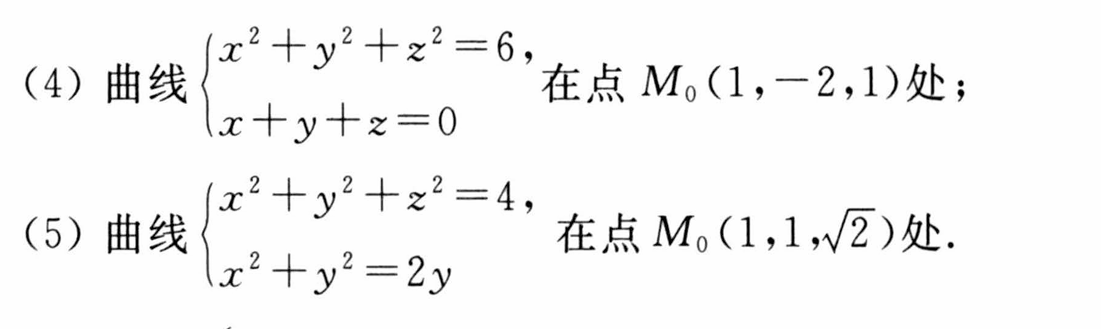
切平面与法向量

7.8 多元函数的极值
课后习题简单回顾
期末考试复习
多元数量值函数积分学及其应用
8.1 二重积分的概念与性质
课后习题简单回顾
微积分下
http://example.com/微积分下/